Conceptos Básicos, Fuerzas Coplanares, Componentes Rectangulares, Suma de Vectores
24/11/2015
Conceptos Básicos
FÍSICA.
La
física es el estudio de las interacciones de la materia con materia o con la
energía. Es una ciencia fundamental relacionada en la comprensión de los
fenómenos naturales que ocurran en el universo. Como todas las ciencias la
física parte de las observaciones experimentales y mediciones cuánticas. El
principal objetivo de la física es utilizar el limitado número de leyes que
gobiernan los fenómenos naturales para desarrollar teorías que puedan predecir
los resultados de futuros experimentos. Las leyes fundamentales empleadas en el
desarrollo de teorías se expresan en el lenguaje de las matemáticas. La física
se divide en física clásica y física moderna.
LA FÍSICA CLÁSICA equivale a toda la física desarrollada antes de 1990,
esta incluye las teorías, conceptos, leyes y experimentos de la mecánica
clásica, la termodinámica y el electromagnetismo es desarrollado hasta finales
del siglo XIX. Los principales contribuyentes de esta física clásica son:
Galileo Galilei, Johannes Kepler e Isaac Newton entre otros.
LA FÍSICA MODERNA se inició a finales de XIX, se desarrolló
gracias a que muchos fenómenos físicos no podían ser explicados por la física
clásica. Los desarrollos más importantes de esta era son la teoría de la
relatividad (Albert Einstein) y la mecánica cuántica.
Fuente: Ciencias
Naturales y Educación Ambiental Asignatura: Física Docente: Erasmo Gaona
Contreras Grado: Décimo
En
muchos sistemas de medida, la longitud es una unidad fundamental, de la cual
derivan otras. Sin embargo, según la teoría especial de la relatividad (Albert
Einstein, 1905), la longitud no es una propiedad intrínseca de ningún objeto,
dado que dos observadores podrían medir el mismo objeto y obtener resultados
diferentes.
Tiempo: El tiempo es una
magnitud física fundamental, el cual puede ser medido utilizando un
proceso periódico, entendiéndose como un proceso que se repite de una manera
idéntica e indefinidamente.
http://conceptodefinicion.de/tiempo/
Masa:
Como masa designamos
la magnitud física con que medimos la cantidad de materia que contiene un
cuerpo. Como tal, su unidad, según el Sistema Internacional de Unidades, es el
kilogramo (kg). Cantidad
mesurable de materia que forma un cuerpo, cuyo valor depende de la resistencia
que dicho cuerpo opone a modificar su estado de reposo o de movimiento y de la
fuerza de atracción que se produce entre ese y otros cuerpos.
Fisica
Ii. Un Enfoque Constructivista - Página 92
https://books.google.com.mx/books?isbn=9702609097
Fuerza:
Cuando hablamos de fuerza, estamos
refiriendo a una magnitud física que se manifiesta de manera lineal y
representa la intensidad de intercambio entre dos partículas o cuerpos (sistema
de partículas). A partir de la fuerza, se puede modificar el movimiento o la
forma de los cuerpos. La fuerza, como magnitud, tiene un sistema de unidad y
puede manifestarse de diferentes maneras.
Dentro del SIU (Sistema Internacional de Unidades) la fuerza es representada por el newton, que es su unidad de medida, cuyo símbolo es N (ene mayúscula). Este nombre se debe a quien ha realizado significativos aportes en la física respecto al estudio de las fuerzas, el científico Isaac Newton
Dentro del SIU (Sistema Internacional de Unidades) la fuerza es representada por el newton, que es su unidad de medida, cuyo símbolo es N (ene mayúscula). Este nombre se debe a quien ha realizado significativos aportes en la física respecto al estudio de las fuerzas, el científico Isaac Newton
El Newton es la unidad de fuerza en el Sistema Internacional de Unidades.
Se
define como la fuerza que aplicada durante un segundo a una masa de 1 kg
incrementa su velocidad en 1 m/s.
Definicion.mx: http://definicion.mx/fuerza/
newton.cnice.mec.es/newton2/Newton_pre/escenas/fuerzas_presiones/queeselnewton.php
Vectores coplanares
Son
aquellos que se encuentran contenidos en un mismo plano
Vectores colineales:
En el caso de
los vectores colineales, se trata
de aquellos que aparecen en la misma recta o que resultan paralelos a una cierta recta. Cuando las
relaciones que mantienen sus coordenadas son iguales y el producto vectorial es
equivalente a 0, dos vectores son colineales
Lee todo en: Definición de vectores colineales - Qué es, Significado y Concepto http://definicion.de/vectores-colineales/#ixzz3sLutW7gc
Introducción
a la geometría y cinemática de medios contínuos
https://books.google.com.mx/books?isbn=8483173778
Vectores concurrentes:
Los
vectores pueden clasificarse de distinto modo de acuerdo a sus características. Se llama vectores
concurrentes a
aquellos que atraviesan un mismo punto.
Debido a que, al pasar por dicho punto dan lugar a la creación de un ángulo, los vectores
concurrentes también se denominan vectores angulares
Lee todo en: Definición de vectores concurrentes - Qué es, Significado y Concepto http://definicion.de/vectores-concurrentes/#ixzz3sLveWtq2
Eficacia
y técnica deportiva: análisis del movimiento humano
https://books.google.com.mx/books?isbn=8487330207
Vectores paralelos:
Dos vectores son paralelos cuando tienen la misma dirección. Es decir que deben estar contenidos en rectas paralelas. En particular cuando dos vectores tienen misma dirección y sentido contrario se dice que son vectores anti paralelos.
https://www.google.com.mx/search?q=que+son+vectores+paralelos&noj=1&biw=1777&bih=838&source=lnms&tbm=isch&sa=X&ved=0ahUKEwifqMmbwqfJAhUDRCYKHfEJBgAQ_AUICCgB&dpr=0.9#imgrc=PSyygmxywIIiXM%3A
Análisis
vectorial. Volumen I: vectores - Página 41
Características de los vectores:
- Magnitud (intensidad) : Tamaño
- Dirección: Ubicación en el plano
- Sentido: A donde apunta la flecha
https://www.google.com.mx/search?q=vectores+caracteristicas&espv=2&biw=1777&bih=887&tbm=isch&imgil=-beLEUto_JnEVM%253A%253Bu_TMUKJLUvCGHM%253Bhttp%25253A%25252F%25252Fwww.uaeh.edu.mx%25252Fscige%25252Fboletin%25252Fprepa2%25252Fn1%25252Fr3.html&source=iu&pf=m&fir=-beLEUto_JnEVM%253A%252Cu_TMUKJLUvCGHM%252C_&dpr=0.9&usg=__f3Rb74H769N68TzxAECQ3ftNZFY%3D&ved=0ahUKEwjep4LI26nJAhUBXGMKHRP3DboQyjcIPQ&ei=5q9UVt6cBYG4jQOT7rfQCw#imgrc=-beLEUto_JnEVM%3A&usg=__f3Rb74H769N68TzxAECQ3ftNZFY%3D
Fuerzas Coplanares
Se encuentran en un mismo plano y en dos ejes, a diferencia de los no coplanares que se encuentras en mas de un plano es decir en 3 ejes.
Pueden indentificarse competamente con sus coordenadas. Una fuerza representa la acción de un cuerpo sobre otro y se caracteriza por tener:
- Magnitud o intensidad.
- Dirección.
- Sentido.
- Punto de aplicación.
Componentes Rectangulares
En un sistema
coordenado de dos dimensiones, cualquier vector puede separarse
en el componente x y el componente y.
Por ejemplo, en la
figura siguiente mostrada, el vector
se separa en dos componentes, vx y vy .
Digamos que el ángulo entre el vector y su componente x es θ.
El vector y sus
componentes forman un triángulo rectángulo como se muestra a continuación.
En la figura
anterior, los componentes pueden leerse rápidamente. El vector en la forma
componente es
.
Las relaciones
trigonométricas dan la relación entre la magnitud del vector y
los componentes del vector.
vx = v cos θ
vy = v sin θ
Aquí, los números
mostrados son las magnitudes de los vectores.
Caso 1: Dados los componentes
de un vector, encuentre la magnitud y la dirección del vector.
Use las fórmulas
siguientes en este caso.
La magnitud del
vector es
.
Para encontrar la
dirección del vector, resuelva
for θ.
Caso 2: Dada la magnitud y la
dirección de un vector, encuentre los componentes del vector.
Use las fórmulas
siguientes en este caso.
vx = v cos θ
vy = v sin θ
http://hotmath.com/
Suma de Vectores
La suma de vectores es sencilla, los vectores tienen módulo y dirección, al sumar 2 vectores por ejemplo A y B nos dará como resultado un tercer vector C. Veamos un ejemplo:
Tres sogas A, B y C están atadas a una estaca y sobre ella actúan 3 fuerzas como se indica en la figura. Determina la fuerza resultante.
Para poder determinar la fuerza resultante es necesario sacar de manera individual las fuerzas de A, B y C de la siguiente manera.
| VECTOR | θ | Fx | Fy | |
| A | 50 N | 0º | (50)(cos0º)=50 | (50)(sin0º)=0 |
| B | 40 N | 140º | (40)(cos140º)=30.641 | (40)(sin140º)=25.7115 |
| C | 60 N | 232º | (60)(cos232º)=36.939 | (60)(sin232º)=-47.280 |
| Rx=-17.58 | Ry=-21.5685 | |||
Ahora que tenemos los resultados individuales, aplicaremos la siguiente formula:
| R= √(Rx)2+(Ry)2 | Tan θ = |Ry/Rx| |
| R=√(-17.58)2+(-21.5685)2 | θ = tan-1 |Ry/Rx| |
| R=√774.2565 | θ= tan-1 |-21.5685/-17.58| |
| R=27.82 N | θ= tan-1 |1.22| |
| θ= 50.65o |
El resultado sería un cuarto vector: D. Como se muestra en la siguiente figura.
Conceptos, Movimiento rectilíneo uniforme (M.R.U.), Movimiento rectilíneo uniformemente acelerado (M.R.U.A.) Caída Libre y Video. 1/12/15
Conceptos.
MOVIMIENTO:
Cambio de la posición de un cuerpo a lo largo del tiempo o espacio.
TRAYECTORIA:
Lugar geométrico de las posiciones sucesivas por las que pasa un cuerpo en movimiento.
MOVIMIENTO RECTILÍNEO:
Es la trayectoria de un cuerpo en linea recta.
MOVIMIENTO CIRCULAR:
Se basa en un eje de giro y radio constante, su trayectoria es una circunferencia.
VELOCIDAD:
Está dada por la relación entre el desplazamiento de un cuerpo en determinado espacio de tiempo, puede ser considerada una magnitud que mide cuan rapido un cuerpo se desplaza.
RAPIDEZ:
La relación entre distancia recorrida y el tiempo empleado en recorrerla.
DISTANCIA:
El espacio que recorre un objeto durante su movimiento.
DESPLAZAMIENTO:
Cambio de posición de un cuerpo entre dos instantes o tiempos bien definidos.
Movimiento rectilíneo uniforme (M.R.U)
 d= v . t d = (12 m/s) (23min.)
d= v . t d = (12 m/s) (23min.)
Movimiento rectilíneo uniformemente acelerado (M.R.U.A.)
El movimiento rectilíneo uniformemente acelerado (m.r.u.a.), también conocido como movimiento rectilíneo uniformemente variado (m.r.u.v), es un movimiento rectilíneo con aceleración constante, y distinta de cero.
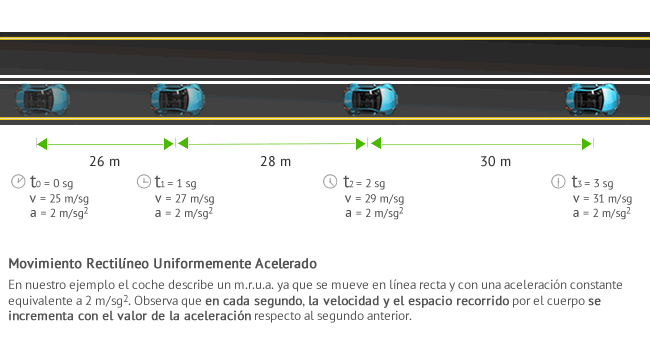
https://www.fisicalab.com/apartado/mrua-ecuaciones#contenidos
El tiro vertical, cuya dirección puede
ser descendente o ascendente, tiene una velocidad inicial que
resulta diferente a cero. El cuerpo en cuestión se lanza hacia arriba,
impulsado con una cierta velocidad. Luego regresa al punto de partida con la
misma velocidad, aunque en un sentido contrario a la que tenía en el momento
del lanzamiento.
Conceptos.
MOVIMIENTO:
Cambio de la posición de un cuerpo a lo largo del tiempo o espacio.
TRAYECTORIA:
Lugar geométrico de las posiciones sucesivas por las que pasa un cuerpo en movimiento.
MOVIMIENTO RECTILÍNEO:
Es la trayectoria de un cuerpo en linea recta.
MOVIMIENTO CIRCULAR:
Se basa en un eje de giro y radio constante, su trayectoria es una circunferencia.
VELOCIDAD:
Está dada por la relación entre el desplazamiento de un cuerpo en determinado espacio de tiempo, puede ser considerada una magnitud que mide cuan rapido un cuerpo se desplaza.
RAPIDEZ:
La relación entre distancia recorrida y el tiempo empleado en recorrerla.
DISTANCIA:
El espacio que recorre un objeto durante su movimiento.
DESPLAZAMIENTO:
Cambio de posición de un cuerpo entre dos instantes o tiempos bien definidos.
Movimiento rectilíneo uniforme (M.R.U)
El movimiento
rectilíneo uniforme (m.r.u.) es aquel en el que la trayectoria es una
linea recta y la velocidad es constante. En este apartado vamos a explicar:
Definición de m.r.u.
A pesar de que
encontrar el movimiento rectilíneo uniforme o m.r.u en
la naturaleza es bastante extraño, es el movimiento más fácil de estudiar y nos
servirá para estudiar otros más complejos.
El movimiento rectilíneo
uniforme cumple las siguientes propiedades:
- La aceleración es cero (a=0)
al no cambiar la velocidad de dirección ni variar su módulo
- Por otro lado, la velocidad
inicial, media e instantánea del movimiento tienen el mismo valor
en todo momento
Un cuerpo realiza un movimiento rectilíneo uniforme cuando su trayectoria es una línea recta y su
velocidad es constante. Esto implica que recorre distancias iguales en
tiempos iguales
Para poder calcular la velocidad de un objeto tenemos la siguiente formula:
Donde:
- V es Velocidad
- D es distancia
- T es tiempo
ejemplos:
- ¿Cual será la velocidad de un tren que recorre 630 km en 7 horas?
v = d/t v= 630km/7h v=90km/h
- ¿Qué distancia recorre un ciclista en 23 min. si lleva una velocidad de 12 m/s?
d=(12) (1380) d=16,560 m.
- Una lancha de motor desarrolla una velocidad de 26.5 m/s ¿cuanto tiempo tardará en recorrer una distancia de 2km?
t=d/v t=2000m/26.5m/s t=75.4 s.
https://www.fisicalab.com/apartado/mru-ecuaciones#contenidos
Movimiento rectilíneo uniformemente acelerado (M.R.U.A.)
El movimiento rectilíneo uniformemente acelerado (m.r.u.a.), también conocido como movimiento rectilíneo uniformemente variado (m.r.u.v), es un movimiento rectilíneo con aceleración constante, y distinta de cero.
Encontrar el movimiento rectilíneo uniformemente acelerado (m.r.u.a.) en tu día a día es bastante común. Un objeto que dejas caer y no encuentra ningún obstáculo en su camino (caida libre) ó un esquiador que desciende una cuesta justo antes de llegar a la zona de salto, son buenos ejemplos de ello. El movimiento rectilíneo uniformemente acelerado (m.r.u.a.) es también conocido como movimiento rectilíneo uniformemente variado (m.r.u.v) y cumple las siguientes propiedades:
- La trayectoria es una línea recta y por tanto, la aceleración normal es cero
- La velocidad instantánea cambia su módulo de manera uniforme: Aumenta o disminuye en la misma cantidad por cada unidad de tiempo. Esto implica el siguiente punto
- La aceleración tangencial es constante. Por ello la aceleración media coincide con la aceleración instantánea para cualquier periodo estudiado (
a=am )
Un cuerpo realiza un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) cuando su trayectoria es una línea recta y suaceleración es constante y distinta de 0. Esto implica que la velocidad aumenta o disminuye su módulo de manera uniforme.

Observa que, aunque coloquialmente hacemos distinción entre un cuerpo que acelera y otro que frena, desde el punto de vista de la Física, ambos son movimientos rectilíneos uniformemente variados. La única diferencia es que mientras que uno tiene una aceleración positiva, el otro la tiene negativa.
Ecuaciones de M.R.U.A.
Las ecuaciones del movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) son:
Donde:
- x, x0: La posición del cuerpo en un instante dado (x) y en el instante inicial (x0). Su unidad en el Sistema Internacional (S.I.) es el metro (m)
- v,v0: La velocidad del cuerpo en un instante dado (v) y en el instante inicial (v0). Su unidad en el Sistema Internacional es el metro por segundo (m/s)
- a: La aceleración del cuerpo. Permanece constante y con un valor distinto de 0. Su unidad en el Sistema Internacional es el metro por segundo al cuadrado (m/s2)
- t: El intervalo de tiempo estudiado. Su unidad en el Sistema Internacional es el segundo (s)
Aunque las anteriores son las ecuaciones principales del m.r.u.a. y las únicas necesarias para resolver los ejercicios, en ocasiones resulta útil contar con la siguiente expresión:
La fórmula anterior permite relacionar la velocidad y el espacio recorrido conocida la aceleración y puede ser deducida de las anteriores, tal y como puede verse a continuación.
Deducción ecuaciones m.r.u.a.
Para deducir las ecuaciones del movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) hay que tener en cuenta que:
- La aceleración normal vale cero:
an=0 - La aceleración media, la aceleración instantánea y la aceleración tangencial tienen el mismo valor:
a=am=at=cte
Con esas restricciones nos queda:
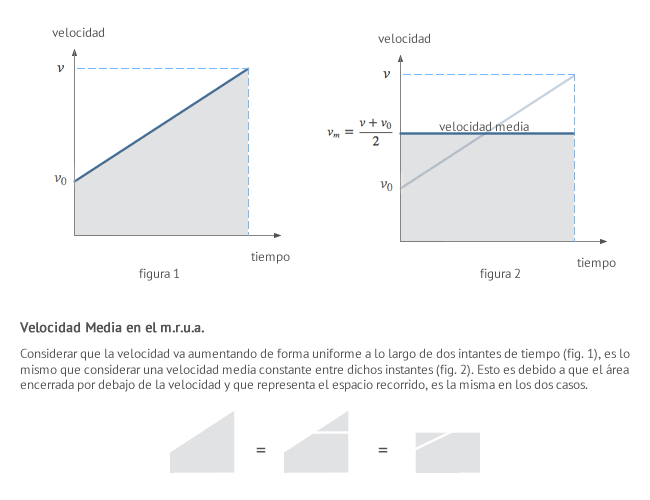
Esta primera ecuación relaciona la velocidad del cuerpo con su aceleración en cualquier instante de tiempo y se trata de una recta (v) cuya pendiente coincide con la aceleración y cuya coordenada y en el origen es la velocidad inicial (v0). Nos faltaría por obtener una ecuación que nos permita obtener la posición. Para deducirla hay distintos métodos. Nosotros usaremos el teorema de la velocidad media o teorema de Merton:
"Un cuerpo en movimiento uniformemente acelerado recorre, en un determinado intervalo de tiempo, el mismo espacio que sería recorrido por un cuerpo que se desplazara con velocidad constante e igual a lavelocidad media que el primero"
Esto implica que:
El valor de la velocidad media, en el caso de que la aceleración sea constante, se puede observar claramente a partir de la siguiente figura:

Si desarrollamos las ecuaciones vistas hasta ahora obtenemos la ecuación de la posición en el movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.):
Donde hemos aplicado:
Por último, indicarte que en las ecuaciones anteriores se ha considerado que el movimiento se realiza en el eje x. Si nos moviéramos en el eje y, por ejemplo en los movimientos de caida libre o de lanzamiento vertical, simplemente sustituirías la x por la y en la ecuación de posición, quedando:
https://www.fisicalab.com/apartado/mrua-ecuaciones#contenidos
Veamos otro ejemplo:
Un automóvil lleva una velocidad de 8m/s hacia el norte, a los 4 seg. su velocidad es de 15 m/s. Determina la aceleración en ese tiempo.
Un automóvil lleva una velocidad de 8m/s hacia el norte, a los 4 seg. su velocidad es de 15 m/s. Determina la aceleración en ese tiempo.
| a= | 15m/s - 8m/s | 7 | =1.75 m/s2 | |
| 4seg | 4 |
La noción de tiro vertical aparece en el campo de
la física. Se trata de un movimiento rectilíneo
uniforme variado, también conocido como MRUV. En un tiro vertical,
la velocidad cambia y existe una aceleración que está dada por la
acción de la gravedad.
Lee todo en:
Definición de tiro vertical - Qué es, Significado y Concepto http://definicionEl lanzamiento horizontal es un ejemplo de composición de movimientos en dos dimensiones: un m.r.u. en el eje horizontal y un m.r.u.a. en el vertical. En este apartado veremos:
Tiro parabólico
Se trata de un “movimiento rectilíneo uniforme” en su desarrollo
horizontal y un “movimiento uniformemente variado” en su desarrollo vertical.
En el eje vertical se comporta como el movimiento de “Tiro
vertical”.
Otro tipo de movimiento sencillo que se observa frecuentemente
es el de una pelota que se lanza al aire formando un ángulo con la horizontal.
Debido a la gravedad, la pelota experimenta una aceleración constante dirigida
hacia abajo que primero reduce la velocidad vertical hacia arriba que tenía al
principio y después aumenta su velocidad hacia abajo mientras cae hacia el
suelo. Entretanto, la componente horizontal de la velocidad inicial permanece
constante (si se prescinde de la resistencia del aire), lo que hace que la
pelota se desplace a velocidad constante en dirección horizontal hasta que
alcanza el suelo. Las componentes vertical y horizontal del movimiento son
independientes, y se pueden analizar por separado. La trayectoria de la pelota
resulta ser una parábola.
Es un movimiento cuya velocidad inicial tiene componentes en los
ejes "x" e "y", en el eje "y" se comporta como
tiro vertical, mientras que en el eje "x" como M.R.U.
Características de las componentes según los ejes:
Eje
|
v
|
a
|
x
|
constante
|
0
|
y
|
9,81 m/s²
|
g
|
Ecuaciones del movimiento según los ejes:
Eje "x" (MRU)
|
Eje "y" (MUV)
|
|||||
1)
|
v = Δx/t
|
Ecuación de velocidad
|
1)
|
yf =
y0 + v0.t
+ ½.g.t²
|
Ecuación de posición
|
|
2)
|
vf =
v0 + g.t
|
Ecuación de velocidad
|
||||
3)
|
vf² = v0² + 2.g.Δy
|
|||||
Ecuaciones de la trayectoria:
Posición
|
x = (v0.cos θ0).t
y = (v0.sen θ0).t - ½.g.t²
|
Velocidad
|
vx =
v0.cos θ0
vy =
v0.sen θ0 -
g.t
|
Altura máxima: como se explicó
anteriormente, el comportamiento en el eje “y” es el característico del “Tiro
vertical”, por lo tanto, para el cálculo de la altura máxima se emplean
las mismas ecuaciones.
1)
|
y Máxima = y0 + v0.t + ½.g.t²
|
Ecuación de posición
|
2)
|
0 = v0 +
g.t
|
Ecuación de velocidad
|
3)
|
0 = v0² + 2.g.Δy
|
Recordar que el valor de la aceleración de la gravedad depende
del paralelo (latitud) en que se determine dicho valor. En el ecuador (latitud
= 0) la aceleración es igual a “9,78049 m/s²”, la aceleración promedio es de 9,81 m/s², es usual usar un valor de 10 m/s² para
agilizar la resolución de ejercicios.
www.fisicanet.com.ar/fisica/cinematica/ap06_tiro_parabolico.php
Video de Caleidoscopio:
Video de Caleidoscopio:














